Немкин Дмитрий Викторович Дальневосточный федеральный университет, инженерная школа Кафедра кораблестроения и океанотехники
Научный руководитель: С.В. Антоненко, д.т.н., профессор
Один из серьезных вопросов при постановке судна в плавучий док – обеспечение местной прочности корпуса судна и самого плавдока в районе установки опор (кильблоков). Известны случаи различных повреждений, а иногда и серьёзных аварий при постановке судов в док, устранение которых может потребовать значительных затрат [1, 2].
Действительно, при проектировании судна, для обеспечения его общей и местной прочности, в первую очередь учитывают действие тех нагрузок, которые могут встретиться в условиях нормальной эксплуатации (нагрузки от общего изгиба) и порядок которых - 1 МПа. Но давление со стороны доковых опор на порядок выше, т.е. это примерно 10 МПа. Эти усилия воспринимаются днищевым набором судна - вертикальным килем, флорами, стрингерами, представляющие собою, в общем случае, прямоугольные пластины [1].
Если эти усилия вызывают сжатие, изгиб в плоскости пластины или сдвиг, то при определенной их величине может произойти потеря устойчивости пластины (т.н. выпучивание). Вследствие этого при дальнейшем возрастании нагрузки основная ее часть будет передаваться на более жесткие связи, подкрепляющие пластину, что вызовет в этих связях быстрый рост напряжений.
На устойчивость также влияет коррозионный износ. Известно, что владельцы плавучих доков часто сталкиваются с проблемой поддержания местной прочности и устойчивости корпусных конструкций на должном уровне, что тесно связано с вопросом неравномерного распределения коррозионного износа [3].
Существуют известные теоретические решения для определения критических напряжений в пластинах [4, 6]. Важным моментом здесь является направление действия сжимающей нагрузки (вдоль короткой стороны или вдоль длинной).
При постановке в док, очень редко загружается вся кромка пластины по всей длине: она может быть загружена на части длины, реакция опоры может приходиться на две пластины (на одну больше, на другую меньше или даже поровну). Напряженно-деформированное состояние пластины может характеризоваться одновременным сжатием, сдвигом и изгибом. На результат расчета сильно влияют условия закрепления. К тому же, судовые пластины имеют вырезы и подкрепления различной конфигурации.
В результате появляется множество вариантов поведения листовых конструкций дока и докуемого судна при доковых операциях, для которых хотелось бы получить приемлемые численные результаты (величина критической силы, форма потери устойчивости, распределение напряжений и т.д.).
Описание используемого программного обеспечения и конечных элементов
Используемые программы. Для исследования устойчивости был выбран МКЭ, реализованный в программах ANSYS и SolidWorks (модуль Simulation).
Расчеты выполнялись в модуле ANSYS Mechanical (подмодули Structural и Buckling). Оценка влияния различных параметров, таких как размер сетки, толщина пластины, соотношение сторон, проводилась в оптимизационном модуле ANSYS DesignXplorer. Данные модули объединены в расчетной платформе ANSYS Workbench.
В работе также использовался SolidWorks Simulation (ранее — COSMOSWorks) – CAE модуль, основанный на методе конечных элементов и предназначенный для проведения прочностного анализа.
Используемые конечные элементы (КЭ). В программе SolidWorks Simulation для оболочек можно использовать треугольные КЭ 1-го и 2-го порядка, с тремя и шестью узлами соответственно (Fig. 1 – a). В программе ANSYS выбор оболочечных конечных элементов шире, но в данной работе выбор был ограничен основными – треугольным и прямоугольным КЭ 1-го порядка (Fig. 1 – b, c)
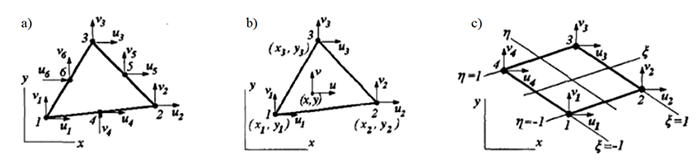
Fig. 1 Типы используемых конечных элементов
Следует отметить, что практика расчетов с применением МКЭ [5] показывает, что сетка треугольных элементов 2-го порядка (с промежуточными узлами на сторонах, fig. 1 - a) имеет, по крайней мере, ту же самую точность, что и сетка прямоугольных элементов с четырьмя узлами (fig. 1 – c). Таким образом, сетка с прямоугольными элементами более предпочтительна, чем сетка с треугольными элементами, т.к. имеет меньшее количество узлов.
Алгоритм исследования
Конечно-элементный модель состоит из нескольких компонентов которые вместе описывают реальную физическую модель. Как минимум, анализируемая модель должна содержать следующую информацию: геометрия, разбитая на КЭ (КЭ сетка), параметры КЭ, информация о материале, нагрузки и граничные условия, тип анализа (решающей программы).
- Геометрия. Критическая нагрузка определялась при различной толщине пластины (t = 4, 6…12 мм), а также при различном соотношении сторон (γ = 0,1; 0,2…3,5). Расчетные схемы показаны на рис. 2.
- КЭ сетка. Для определения влияния количества узлов КЭ модели на значение критической нагрузки расчетная область разбивалась с разной густотой сетки. При этом, критическая нагрузка определялась также при толщине пластины от 4 до 12 мм.
- Параметры КЭ. При расчете пластин в SolidWorks (SW) Simulation использовались треугольные пластинчатые КЭ с шестью узлами (рис. 1 – а). При расчете в ANSYS были использованы треугольные и прямоугольные КЭ 1-го порядка (рис. 1 – b, c)
- Материал. В качестве материала из стандартной библиотеки SolidWorks была выбрана листовая углеродистая сталь со следующими характеристиками: Модуль упругости, E = 2,05x105 МПа, модуль Юнга, µ = 0,29. В ANSYS был выбран материал с аналогичными характеристиками.
- Внешняя нагрузка. Критическая нагрузка в SW Simulation и ANSYS определяется в виде коэффициента который показывает во сколько раз необходимо увеличить внешнюю нагрузку для того чтобы конструкция потеряла устойчивость. Для определения значений критической нагрузки прикладывались единичные силы (P = 1 Н) к противоположным кромкам пластины. Также было проанализировано влияние ширины приложения нагрузки и её расположения относительно краёв. Ширина нагрузки изменялась от 5% до 95% от ширины пластины.
- Граничные условия. Для оценки влияния условий закрепления пластины на величину критической нагрузки КЭ были выполнены расчеты при различных граничных условиях (жестко заделанная по всем кромкам пластина, свободно-опертая по всем кромкам пластина и несколько промежуточных случаев закрепления). Рис. 2 иллюстрирует расчетные случаи. Подробное описание приведено ниже.
- Тип анализа. Для определения критической нагрузки в программах SW Simulation и ANSYS используется специальный модуль «Buckling analysis».
Влияние количества узлов модели на значения критической нагрузки
Важно использовать достаточно мелкую КЭ сетку для обеспечения точности вычисления. Численное решение зависит от плотности КЭ сетки, что в свою очередь влияет на задействованные вычислительные ресурсы. После некого порога дальнейшее уплотнение КЭ сетки приводит к незначительным изменениям в численном решении.
Для выявления чувствительности результатов расчета критической нагрузки к изменению плотности сетки расчеты выполнялись при размере конечного элемента от 0,5% до 25% от наименьшего размера стороны пластины а (рис. 2), что соответствует плотности сетки от 80 до 160000 узлов в SW Simulation и от 25 до 56000 узлов в ANSYS. Критическая нагрузка определялась при различной толщине и соотношении сторон. Расчетные схемы показаны на рис. 2.
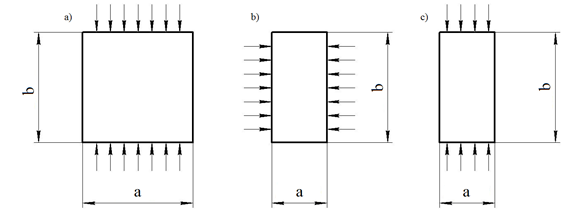
Fig. 2. Расчетные схемы с различным соотношением сторон
На рис. 3, а также на рис. 4 и 5 приведены результаты тестовых расчетов для квадратной пластины (Fig. 2 – a). По оси Y отложена «погрешность» (Δ) значения критической нагрузки полученного по МКЭ в сравнении с аналитическим (справочным) решением: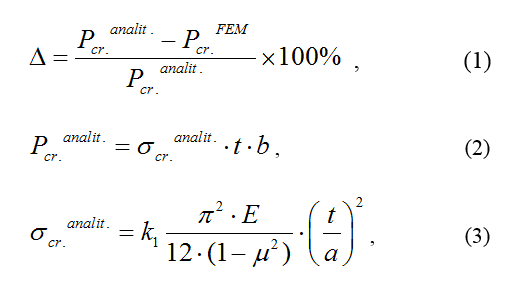
где:
σcr.analit. – аналитическое решение [6];
Pcr.FEM – решение по МКЭ;
k1 – коэффициент, учитывающий соотношение сторон пластины [6];
E – модуль упругости, МПа;
µ – 0,29 - модуль Юнга.
По оси X отложено количество узлов сетки (над осью) и размер КЭ в проценте от наименьшего размера пластины, a (под осью).
Из графиков (рис. 3 – 5) видно, что толщина пластины практически не влияет на устойчивость численного решения при использовании треугольного элемента 2-го порядка (SW Simulation) и прямоугольного элемента 1-го порядка (ANSYS) поэтому на последующих графиках (рис. 6 и 7) приведены результаты при толщине пластины t = 4 мм. Следует отметить существенную погрешность, направленную в опасную сторону при использовании треугольного элемента 1-го порядка даже при достаточно густой сетке (Рис. 4).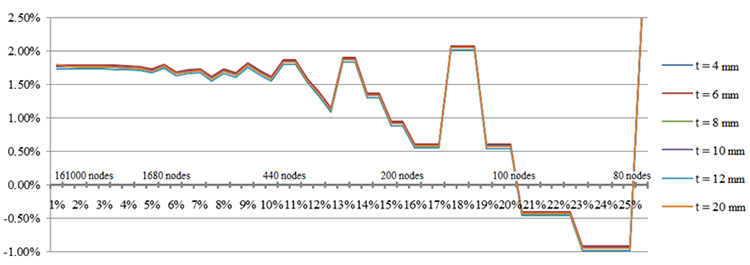
Fig. 3 SW Simulation. Зависимость критической нагрузки от количества узлов сетки при различных толщинах. Треугольный КЭ 2-го порядка (Fig. 1 – a).
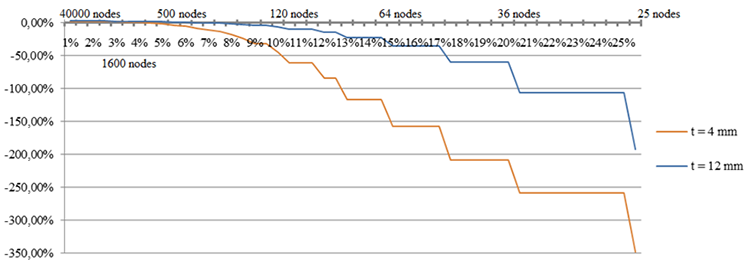
Fig. 4 ANSYS. Зависимость критической нагрузки от количества узлов сетки при различных толщинах. Треугольный КЭ 1-го порядка (Fig. 1 – b)
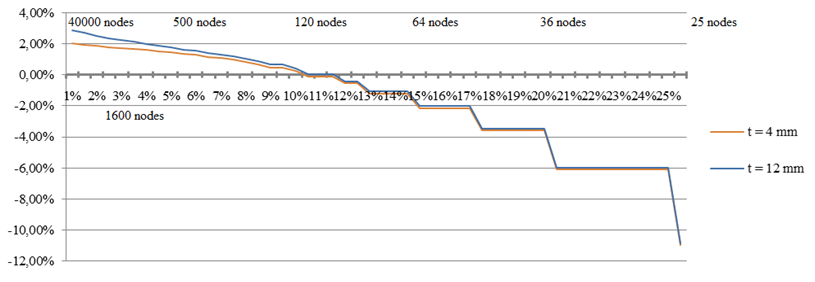
Fig. 5 ANSYS. Зависимость критической нагрузки от количества узлов сетки при различных толщинах. Прямоугольный КЭ 1-го порядка (Fig. 1 – с)
Из графиков (рис. 3 – 5) видно, что с увеличением числа узлов КЭ модели повышается устойчивость решения. И при некотором значении (1500 – 5000 узлов или при размере КЭ от 5% до 2% от размера меньшей стороны пластины), применение более густой сетки практически не влияет на значения критической нагрузки пластины, но значительно увеличивает время проведения расчета.
На рис. 6 приведены результаты расчетов для пластин с различным соотношением сторон (a/b от 0,1 до 3,5). Расчеты выполнены при толщине пластины t = 10 мм.
Критическая нагрузка сравнивалась с результатами, полученными по формуле РС для расчета критических напряжений пластин:
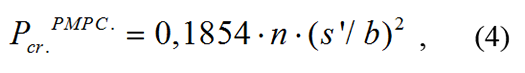
где:
n – коэффициент, зависящий от вида нагружения пластин и отношения сторон;
s’ – построечная толщина пластины, мм;
b – сторона пластины, перпендикулярная направлению действия нормальных сжимающих напряжений, м
Также на графике приведены значения, полученные по формуле (2), при коэффициентах k1, k2 и k3.
Треугольный элемент 1-го порядка на графике не представлен, т.к. погрешность расчета очень существенна. Треугольный элемент 2-го порядка и прямоугольный элемент 1-го порядка использовались в SW Simulation и в ANSYS соответственно.
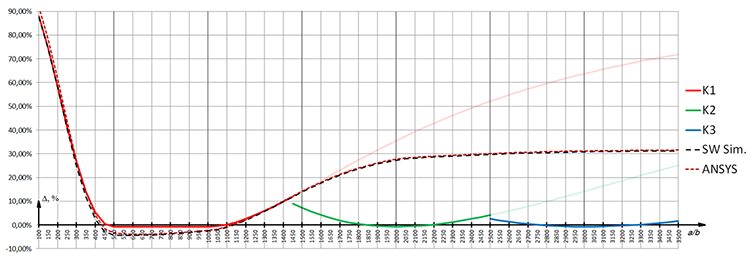
Fig. 6 Зависимость критической нагрузки от соотношения сторон, a/b (свободно-опертая пластина)
Расчеты проводились при достаточно густой сетке (размер КЭ ≤ 5% от меньшего размера стороны пластины). Граничные условия – пластина, свободно опёртая по всем четырем кромкам.
Как видно из графика (рис. 6), численное решение практически совпадает с аналитическими результатами, полученными по формуле (2) при соотношении сторон a/b от 0,1 до 1,5. А при a/b от 0,5 до 1,1 численное и аналитическое решения хорошо согласуются с формулой Морского Регистра (4). Введение в формулу (2) коэффициентов k2 и k3 приводит аналитическое решение в соответствие с формулой Морского Регистра. Численное же решение при соотношении сторон a/b > 1,5 даёт завышенное (на 30%) значение критической нагрузки.
На рис. 7. показаны результаты расчетов для жесткозаделанной пластины с различным соотношением сторон (a/b от 1 до 4). Как видно, погрешность высока и продолжает увеличиваться с ростом отношения. Кроме того, при увеличении отношения сторон a/b (т.е. при «вытягивании» пластины вдоль направления сжимающей нагрузки) критическая нагрузка растёт, в то время как согласно формуле (2), с коэффициентом k4 (табличное значение для жесткозаделанной пластины, [6]) критическая нагрузка уменьшается.
Тем не менее, это всегда хорошая практика, чтобы провести исследование сетки конвергенции, где вы симулируете ту же проблему с более тонкой сеткой и сравниваете результаты. Вы можете быть уверены, что ваша модель производит математически точное решение, если сетки дают по существу один и тот же результат.
Представленные выше расчеты выполнены при свободном опирании пластины по всем четырем кромкам (кроме рис. 7). Оценка влияния других способов закрепления пластины представлена ниже.
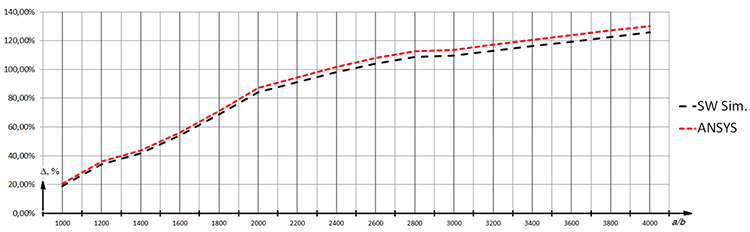
Fig. 7 Зависимость критической нагрузки от соотношения сторон, a/b (жесткозаделанная пластина)
Влияние граничных условий на значения критической нагрузки.
Для оценки влияния условий закрепления пластины на величину критической нагрузки КЭ были выполнены расчеты при различных граничных условиях. На рис. 8 приведены расчетные схемы: a - свободно-опертая по всем кромкам пластина, b – две противоположные кромки свободно оперты, остальные - жестко заделаны, нагрузка приложена к свободно опертым кромкам; c – так же как b, нагрузка приложена к закреплённым кромкам; d – жестко заделанная по всем кромкам пластина.
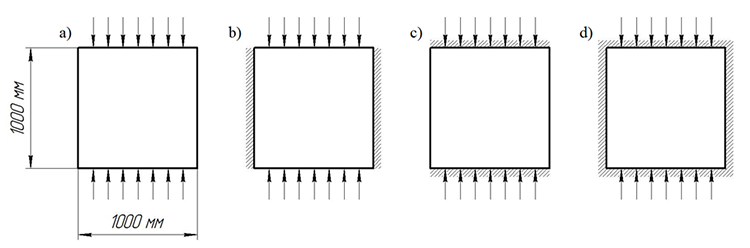
Fig. 8 Расчетные схемы с различными условиями закрепления
На графиках (рис. 9 и 10) приведены результаты расчетов для квадратной пластины толщиной t = 8 мм. На рис. 9 показаны результаты расчетов с использованием треугольного КЭ 2-го порядка, выполненные в SW Simulation. Результаты расчетов при прямоугольном КЭ 1-го порядка, выполненные в ANSYS показаны на рис. 10.
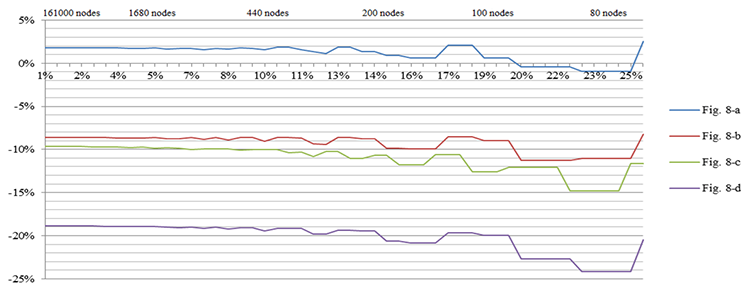
Fig. 9. Зависимость критической нагрузки от количества узлов (SolidWorks Simulation)
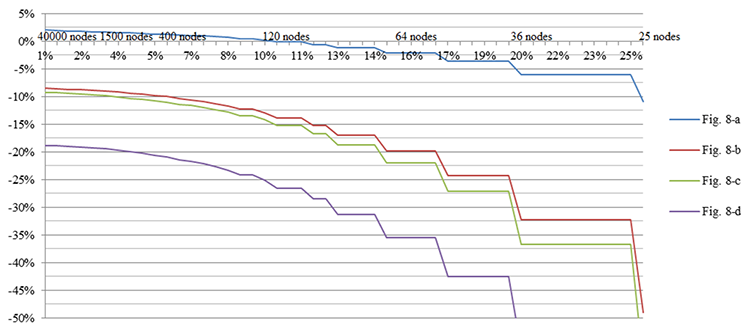
Fig. 10. Зависимость критической нагрузки от количества узлов (ANSYS)
Из графиков видно, что погрешность (Δ) численного решения по сравнению с аналитическим растет при ограничении поворотов на кромках пластины и в случае жестко закрепленной по всем кромкам пластины, Δ достигает 20% в опасную сторону.
Влияние ширины приложения нагрузки и её расположения на значения критической нагрузки.
При анализе устойчивости пластин согласно Правилам РС или используя методы строительной механики корабля, внешняя нагрузка обычно распределена по всей длине пластины.
Однако, при постановке в док, когда вес судна через доковые опорные устройства перераспределяется на конструкции понтонов и днищевые перекрытия самого судна, очень редко загружается вся кромка пластины по всей длине. Она может быть загружена на части длины или реакция опоры может приходиться на две пластины (на одну больше, на другую меньше или поровну, рис. 11).
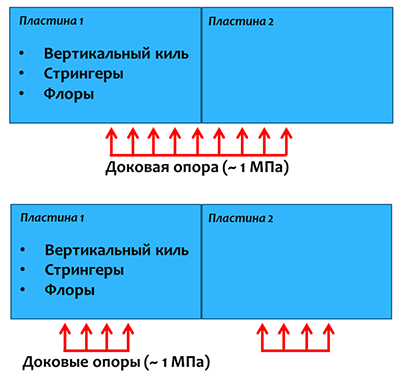
Fig. 11. Нагрузка на пластины перекрытия при постановке судна в док
На рис. 12 показан график изменения критической нагрузки P* от длины загруженной кромки пластины, b. P представлена в процентах от критической силы пластины, загруженной по всей длине.
Из графика видно, что опасным является случай, когда пластина загружена на ¾ своей длины. Критическая нагрузка при этом на 10% меньше того значения, которое мы бы получили при загруженной по всей длине пластины, т.е. как принято в обычной инженерной практике.
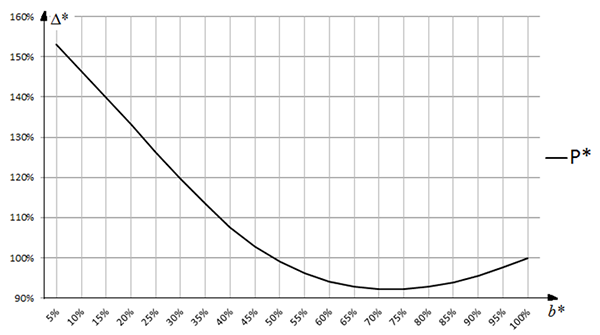
Fig. 12. Изменение критической нагрузки P* в зависимости от длины загруженной кромки, b*.
Кроме того, что нагрузка на пластину может быть распределена не по всей длине кромки, она также может быть смещена на некоторое расстояние от края пластины, b. На графике представлена зависимость P от зазора b*, при длине загруженной кромки, b = 100 мм. P* представлена в процентах от критической силы пластины, загруженной по всей длине.
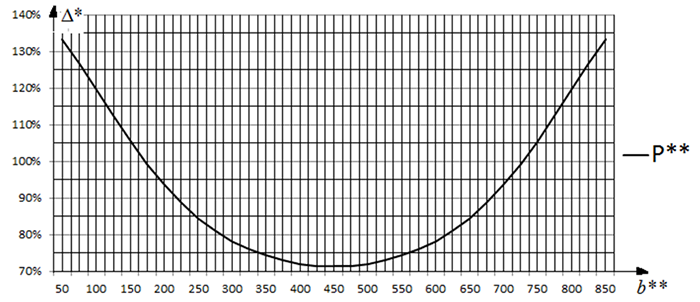
Fig. 13. Изменение критической нагрузки P* в зависимости от расположения нагрузки по длине пластины (длина загруженной кромки, b* = 100 мм).
Выводы
В статье выполнены анализ и сравнение аналитических решений устойчивости пластин с результатами компьютерного моделирования с использованием МКЭ. Показано, что толщина практически не влияет на погрешность численного решения, Δ. Большое влияние на Δ оказывают условия закрепления пластины и при более жестком ограничении поворотов кромок погрешность растет, достигая 20% в случае жесткой заделки даже при очень густой сетке (40 – 160 тыс. узлов).
Также следует отметить существенную погрешность, направленную в опасную сторону при использовании треугольного элемента 1-го порядка даже при достаточно густой сетке. При использовании треугольного КЭ 2-го порядка (с промежуточными узлами на сторонах) и прямоугольного КЭ 1-го порядка устойчивое решение наступает при количестве узлов, n > 1500. Очень густая сетка (n > 50000.) практически не влияет на результат, но значительно увеличивает время проведения расчета.
